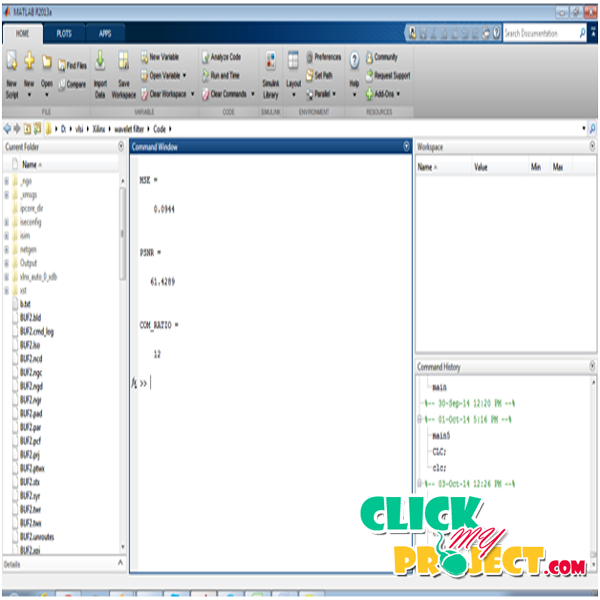
In our project we analyze the performance of orthogonal wavelet filters for image compression on variety of test images. The test images are of different size and resolution. The compression performance is measured, objectively peak signal to noise ratio and subjectively visual quality of image and it is found that orthogonal wavelets outperform. Under normal conditions, the DWT provides near perfect performance, but in situations requiring the transmission of images across noisy or bandwidth-limited channels, the performance of the wavelet algorithm may be improved by redefining the wavelet filter using an optimization algorithm. The discrete wavelet transform has a huge number of applications in science, engineering, mathematics and computer science. In numerical analysis and functional analysis, a discrete wavelet transform (DWT) is any wavelet transform for which the wavelets are discretely sampled. Practical applications can also be found in signal processing of accelerations for wavelet filter in digital communication. and many others. Daub-6 derives is a wavelet filter bank operation. The proposed algorithm optimize the wavelet filter bank architecture. In our architecture we analyze the performance of Daubechies 6-tap wavelet filter banks for image compression on variety of test images. The test images are of different size and resolution. The compression performance is measured, objectively peak signal to noise ratio and subjectively visual quality of image and it is found that Daubechies 6-tap wavelet filter wavelets outperform. The optimized filters provide good performance under special conditions they no longer adhere to the mathematical properties of wavelets, namely the orthogonal between the forward and inverse filters. In our architecture we analyze the performance of orthogonal wavelet filters for image compression on variety of test images. Our Daub-6 filter technique used for the wavelet transform. Daub-6 filter banks give perfect reconstruction filter banks for any number of channels. Orthogonal filter banks are also called paraunitary filter banks. This Daub-6 filter wavelet transform used to reduce the adder counter for the filter architecture. And reduce the path delay also. The test images are of different size and resolution. The compression performance is measured, objectively peak signal to noise ratio and subjectively visual quality of image and it is found that Daub-6 wavelets outperform. This architecture to improve the performance and increase the system speed. In our project developed in Matlab 2013a and VLSI –Xilinx 14.2 domain. The image process to be visualizes using the Matlab software and the filter architecture to be optimized using the Xilinx version-14.2.