Description

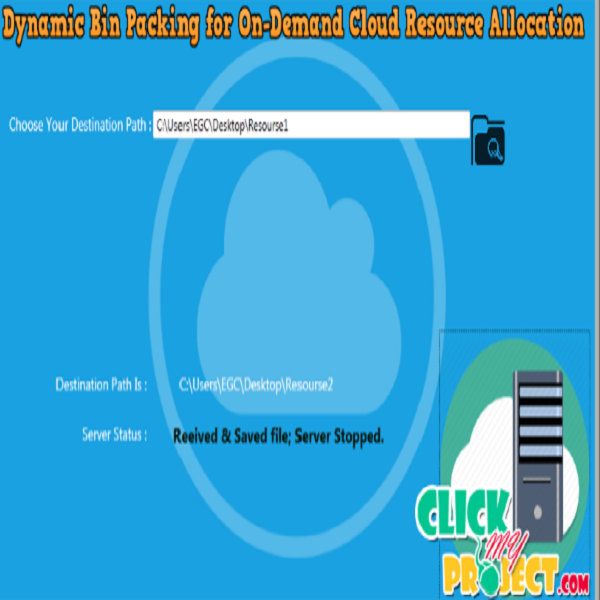
Packet classification is the core mechanism that enables many networking devices. Although using ternary content addressable memory (TCAM) to perform high-speed packet classification has become the widely adopted solution, TCAM is very expensive, has limited capacity, consumes large amounts of power, and generates tremendous amounts of heat because of their extremely dense and parallel circuitry. In this paper, we propose the first packet classification scheme that uses binary CAM (BCAM). BCAM is similar to TCAM except that in BCAM, every bit has only two possible states: 0 or 1; in contrast, in TCAM, every bit has three possible states: 0, 1, or * (don’t care). Because of the high complexity in implementing the extra “don’t care” state, TCAM has much higher circuit density than BCAM. Dynamic Bin Packing (DBP) is a variant of classical bin packing, which assumes that items may arrive and depart at arbitrary times. Existing works on DBP generally aim to minimize the maximum number of bins ever used in the packing. In this paper, we consider a new version of the DBP problem, namely, the MinTotal DBP problem which targets at minimizing the total cost of the bins used over time. It is motivated by the request dispatching problem arising from cloud gaming systems. We analyse the competitive ratios of the modified versions of the commonly used First Fit, Best Fit, and Any Fit packing (the family of packing algorithms that open a new bin only when no currently open bin can accommodate the item to be packed) algorithms for the MinTotal DBP problem. We show that the competitive ratio of Any Fit packing cannot be better than m þ 1, where m is the ratio of the maximum item duration to the minimum item duration. The competitive ratio of Best Fit packing is not bounded for any given m. For First Fit packing, if all the item sizes are smaller than of the bin capacity (b > 1 is a constant), the competitive ratio has an upper bound of. For the general case, the competitive ratio of First Fit packing has an upper bound. We also propose a Hybrid First Fit packing algorithm that can achieve a competitive ratio no larger than 5 4 m þ 19 4 whenm is not known and can achieve a competitive ratio no larger than m þ 5 whenm is known.