Description

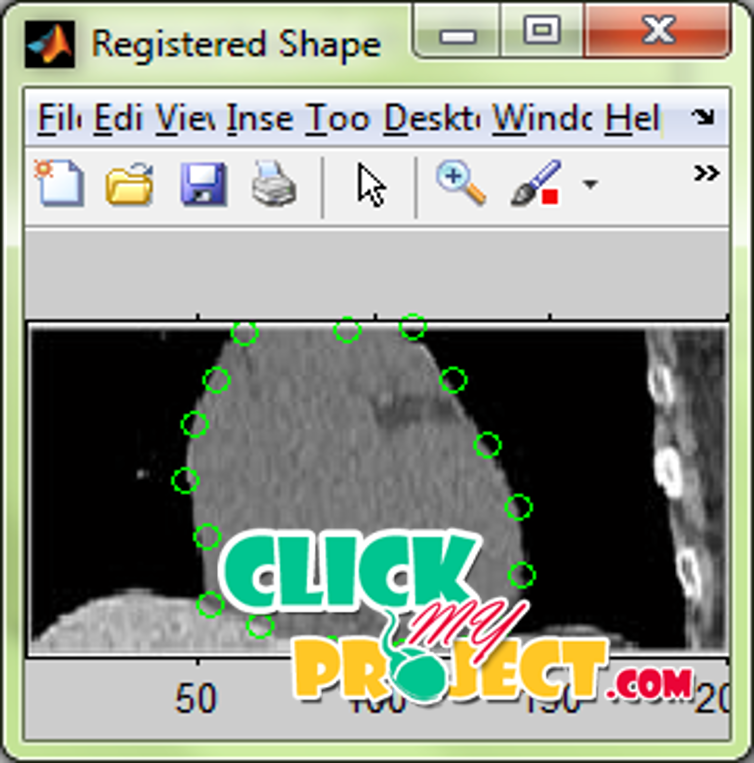
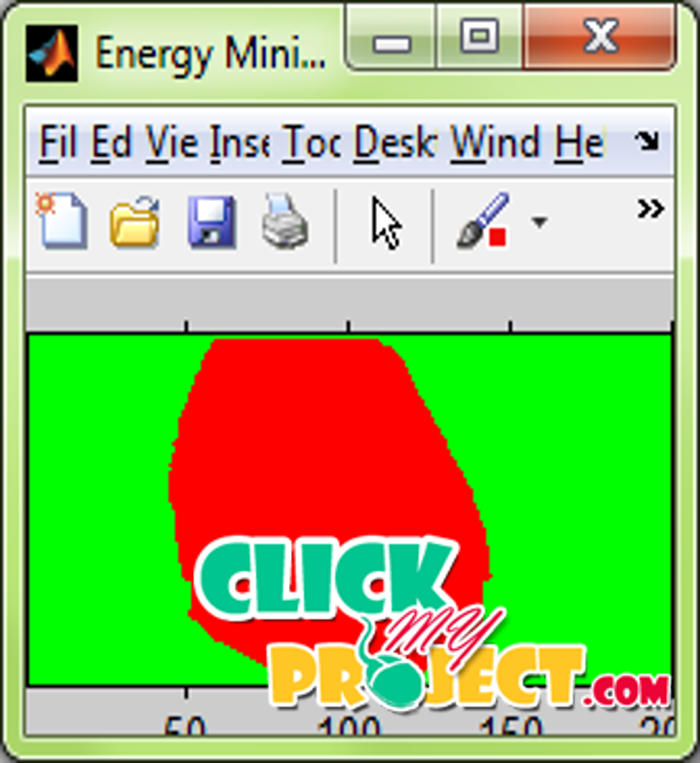
Segmentation is an important task in all kinds of image analysis. In medical image analysis segmentation has a great clinical value since the aim could be to localize organs or pathologies in order to raise the quality of diagnoses. The segmentation of the images has numerous applications in computer vision and other artificial intelligence process. The input non-contrast CT images of heart were taken as the input. The input images were segmented using four different models inorder to obtain the overall segmentation of the heart image with minimized energy. The first step in any energy minimization problem is the identification of the form of the energy function. Some of the popular energy terms were divided into three main categories: boundary, region, and shape. Boundary terms are concerned primarily with the object boundary, region terms with the region inside or outside the object, and shape terms with the shape of the object. Other energy terms include spatial constraints on multipart objects, for example, containment (or layering), exclusion, or the number of labels. As expected, all functions must have domains and so in turn energy functionals must have domains. That domain is the space of possible segmentations of the image or shapes. There are many different ways to represent the underlying segmentation, and that choice in turn impacts the image and shape terms that can be readily evaluated. A substantial amount of knowledge is often available about anatomical structures of interest—characteristic shape, position, orientation, symmetry, relationship to neighboring structures, associated landmarks, etc. and about plausible image intensity characteristics, subject to natural biological variability or the presence of pathology. Once collected, the training data typically come into the energy functional in the place of shape priors. As shape priors have been a particular area of interest in the field. Linear shape models assume the data lies on a linear manifold, but shapes often lie on nonlinear manifolds where the manifold’s properties are not accurately captured by linear statistics. The input images were segmented using four different models that were based on the boundary, edge and shape prior models. The segmentation energy is measured in each case. The final segmentation energy is measured by combining the segmentation energy of all the obtained energy in each segmentation cases. The iterations were repeated so that the segmentation energy is minimized comparing to the segmentation energy obtained in previous iteration. The proposed method is more efficient in the reduction of the segmentation energy comparing to the existing algorithms employed.